这本书说什么?
与其说是介绍数学知识,不如说是介绍数学哲学,作者目的是让我们学习如何抽象地思考。
数学的研究对象?
数学的研究对象是数和空间。数学家并不是将科学理论直接应用于现实世界中,而是应用于模型上。在这里,模型可以看作是所要研究的那部分现实世界的一种虚构、简化的版本。在模型里,我们就有可能进行完全精确的计算。
数学对我有什么用?
锻炼思维,支撑日常的思考和决策。
数学可用于日常思维的概念?
抽象。抽象是把稳定共同的特征提取出来,从片面看到整体。问题太复杂时,尝试进行抽象,在这个过程中也许能看清关键问题。另外,不同表现形式的问题抽象出来可能会简化成同一个模型。生活中的问题被抽象成模型,即所谓的建模。
抽象的方式有很多:在下面的抽象案例中,石头被简化为一个点,人口被简化为一个数,分子间相互作用被假设为根本不存在,大脑被简化为遵循一些简单数学规则的门的网络。
抽象案例1

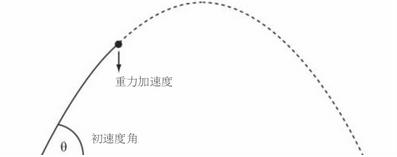
抽象案例2 一开始有5个橘子,吃掉2个,还剩下几个?抽象为:5-2=3
抽象案例3【掷骰子】 我们无法预知每次投掷的结果,但可以回答“两个骰子之和为7的可能性有多大”,在这个过程中,骰子的形状、材料、初始速度、旋转速度都被忽略。
抽象案例4【预测人口增长】 我们在设计模型时假设出生率和死亡率不变,获得一个人口增长预测的公式【n+1人口=n人口*(1+出身率-死亡率)】。这是某种有条件的预测,也就是说模型只能告诉我们,在出生率和死亡率不变的条件下,如果出身率明显死亡率,那么人口将急剧增长。
抽象案例5【气体行为】 伯努利提出模型:N个分子完全相互独立运动,且分子的速度大小都相同。虽然这种模型过度简化,但是依然能解释气体的许多行为。麦克斯韦在这个模型上解决了初始速率的问题,迈进了一大步。 数量减到最少的规则;增加数量后的规则(如果盒中只有一个分子,那么规则可以很明显:分子以恒定速度运动,撞到盒子壁面时就反弹出去。要将这种模型推广到包含N个分子的情形(N是个较大的数),最简单的办法就是假设分子都遵从这样的运动规则,分子之间绝对没有相互作用)
抽象案例6【大脑与计算机的模型化】 计算机的01与计算和大脑的0-1信号强度
下一步阅读方向?
暂无